こんにちは。ころすけです。
飛行機が円を描くように飛行する動作を旋回と言います。
福岡空港や伊丹空港など特定の空港では、周辺の地形問題や騒音対策のため、飛行機が低高度で旋回する様子が頻繁に見られます。
このように飛行機が旋回して向きを変える時、一体どれぐらいの大きさの円を描いているのか気になったことはありませんか?
今回は飛行機が旋回する時の円の大きさについて、理論的に考察してみたいと思います。
飛行機の旋回は円運動!
物体が進行方向を変える動きというのは、物理学的には円運動で説明がなされます。
円運動は進行方向に対して常に直角方向に力が働く場合にきれいな新円を描いた動きになるのですが、この進行方向に対して直角に働く力を「向心力」と言います。
例えば自動車などでは、タイヤの向きを曲がりたい方向に向けて、タイヤが地面を蹴る力を内向きに向けることで向心力を生み出しています。
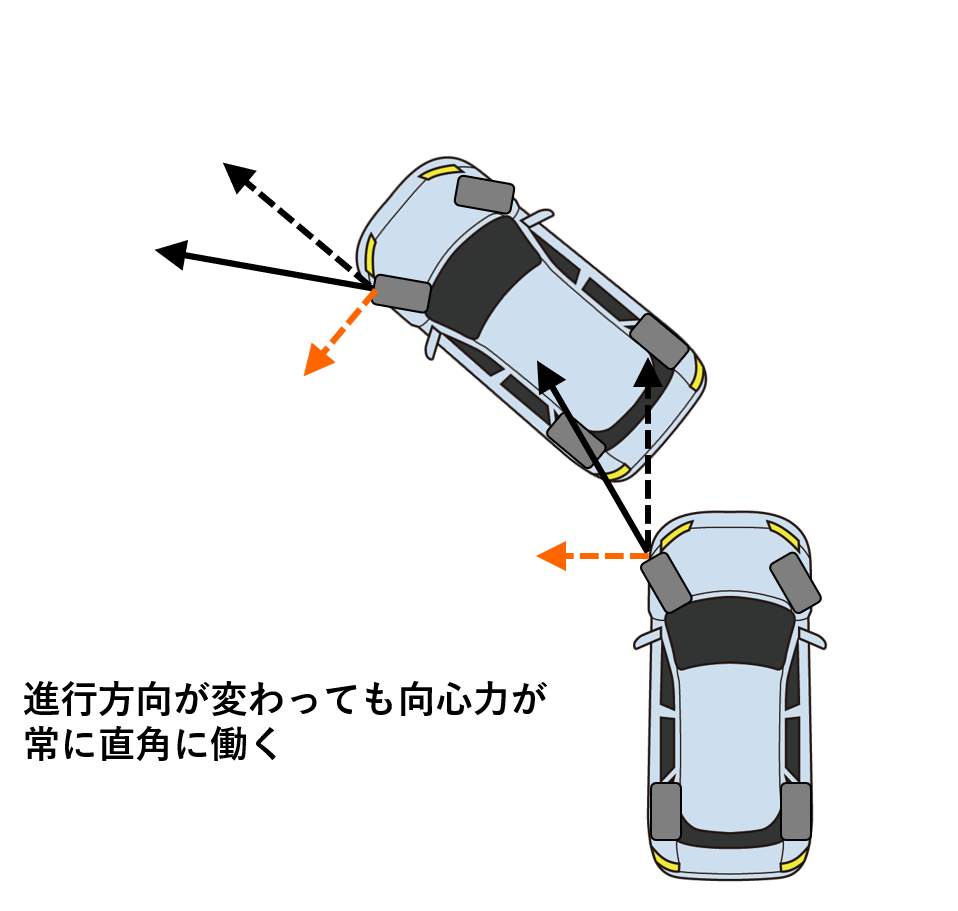
では地面のない飛行機が一体どのように向心力を生み出しているのかと言うと、実は飛行機では自身の姿勢を傾けることで向心力を生み出しているのです。
飛行機が姿勢を傾けると翼に発生している揚力も斜めに傾きますが、この斜めに傾いた揚力の水平方向成分が向心力になるというわけです。
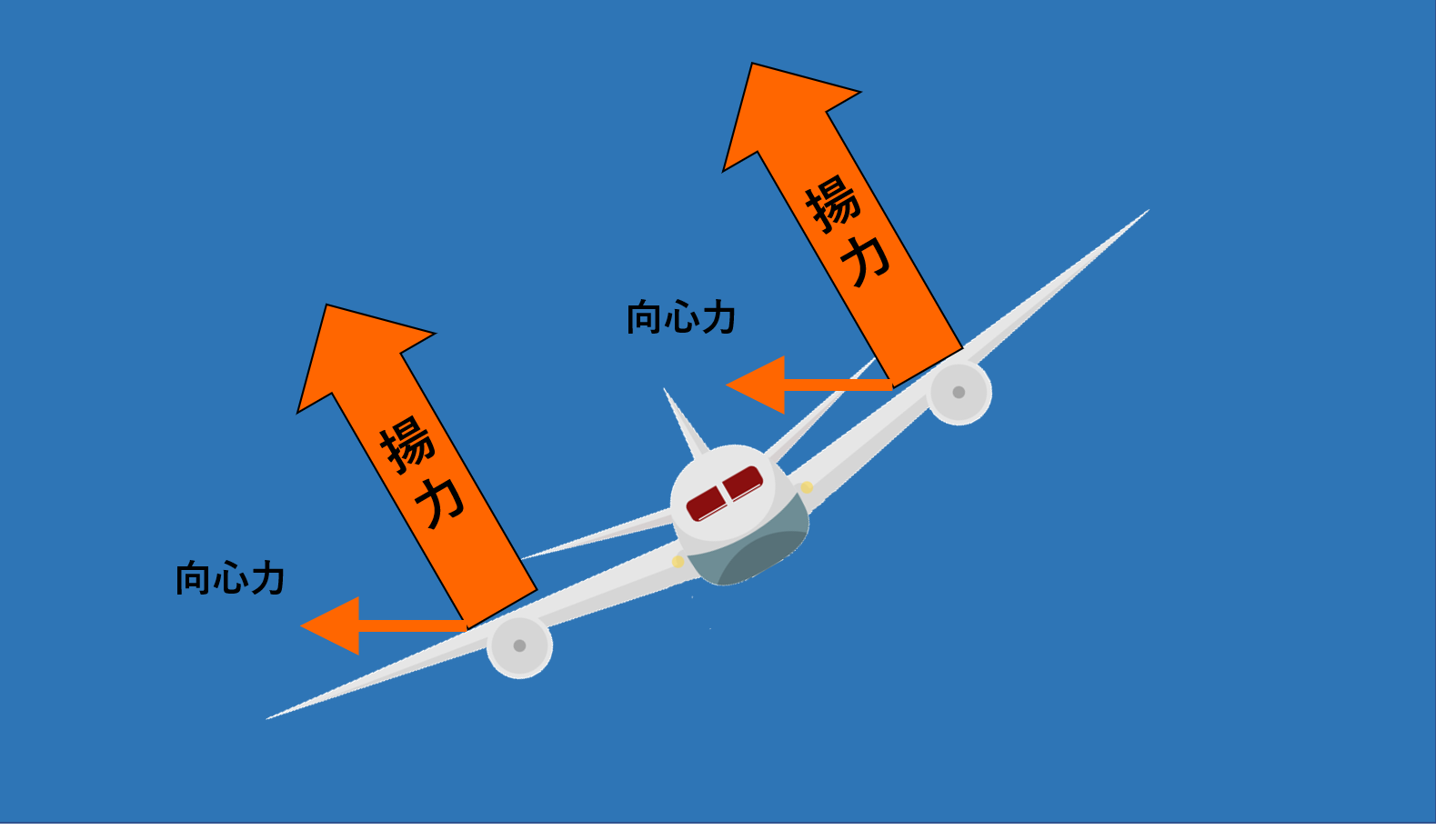
飛行機が旋回する原理については以下の記事で詳しく解説していますので、興味がある方は是非ご覧になってください。

飛行機の旋回半径を求めてみよう!
飛行機の旋回が円運動であると分かれば、あとの考え方は比較的簡単です。
円運動自体は高校物理で習う内容ですから、その通りに数式を解いてやれば良いわけです。
物理を習ったことがないという方には難しいかもしれませんが、「学校で習う学問レベルで飛行機の運動を説明できるんだ」と理解していただくだけでもOKだと思います。
それではさっそく計算してみましょう。
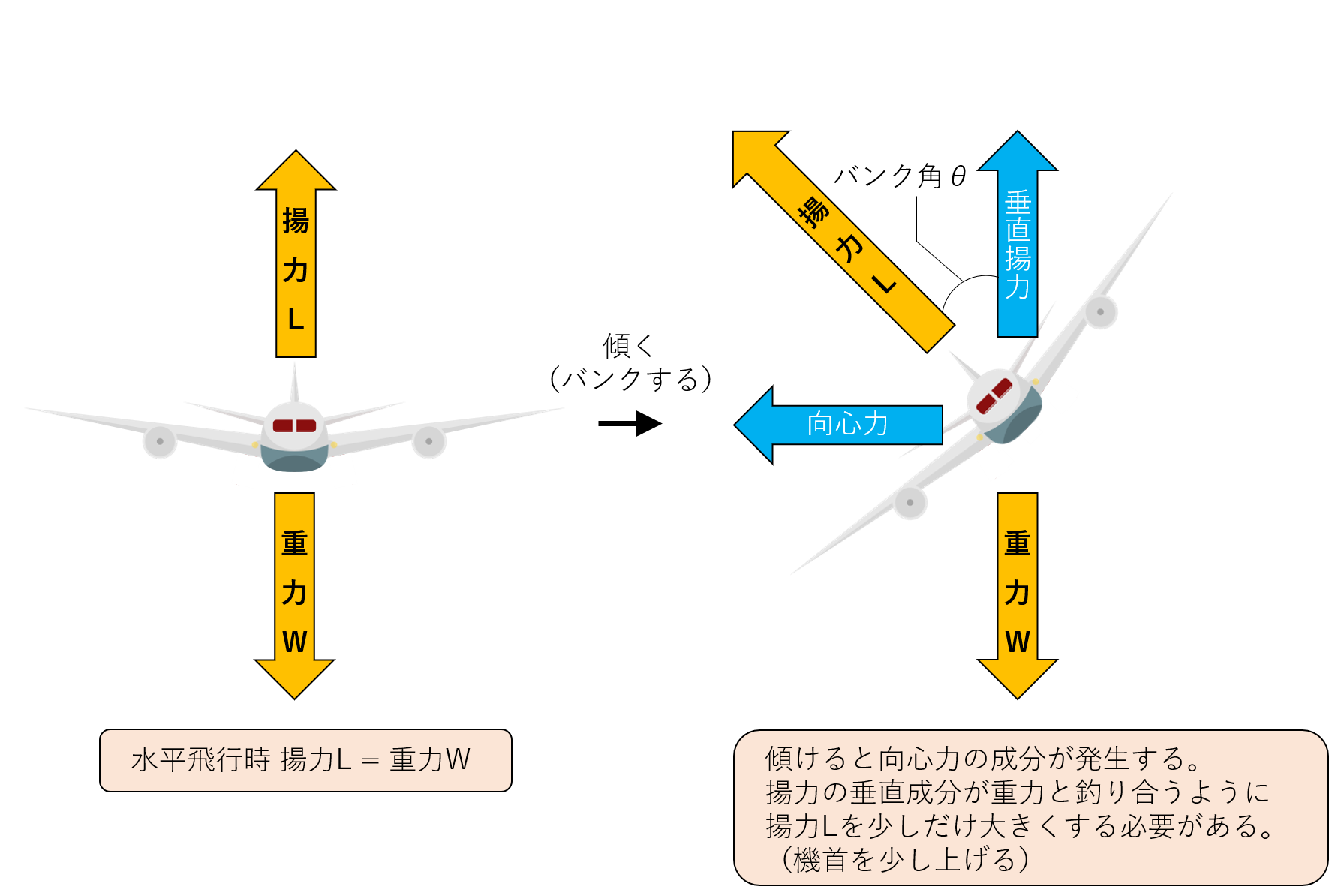
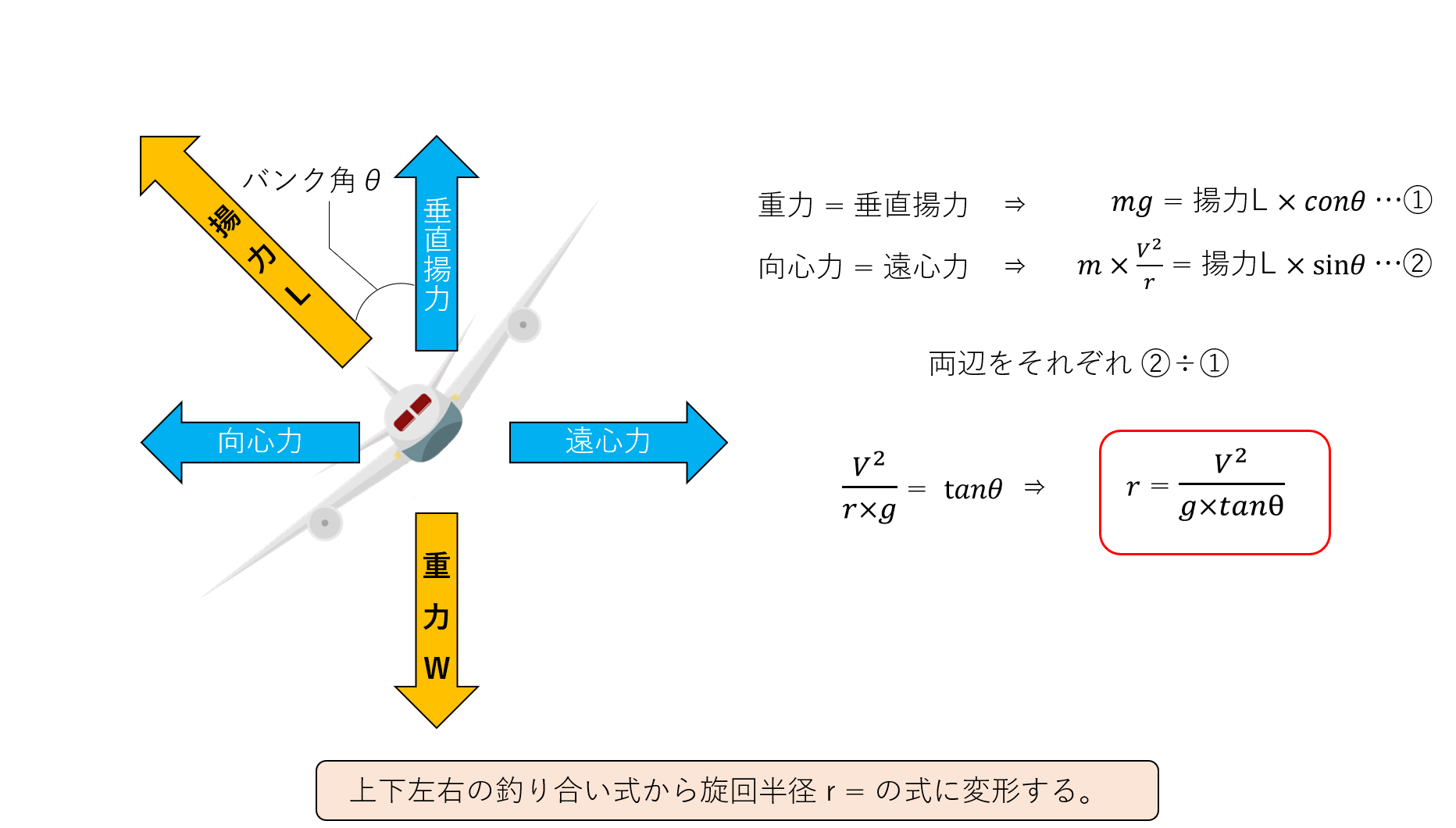
まず、水平飛行している最中(下図左)では、揚力Lと重力Wが釣り合っています。
この状態で機体が傾く(バンクする)と、揚力Lが傾いて水平方向の力の成分(向心力)が発生します(下図右)。
この時、傾いた揚力の垂直方向成分(垂直揚力)で重力Wを支えないといけなくなるので、揚力Lは水平飛行時よりも若干大きくしなければなりません。
揚力は機首を上げると大きくなるのですが、実は旋回中は少しだけ機首を上に上げるのです。
下の図に示すように、向心力や垂直揚力はバンク角の三角関数で表すことができます。
さらに物体が円運動している最中では、向心力と同じ大きさの遠心力が発生しますが、遠心力は物体(飛行機)の質量と速度で表すことができます。 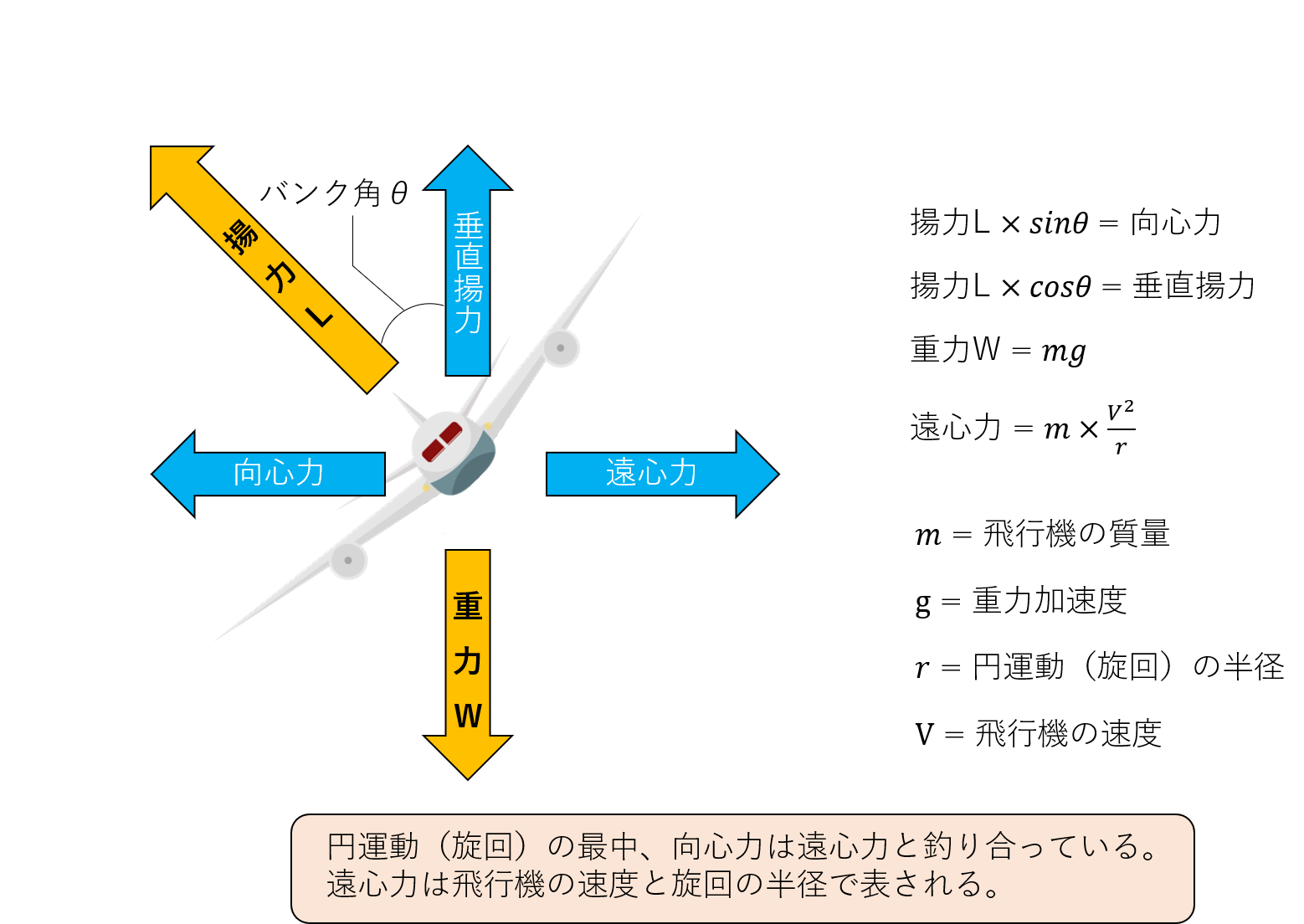
後は上下方向の力の釣り合い(垂直揚力と重力)と水平方向の力の釣り合い(向心力と遠心力)から式を変形するだけです。
式を解いて見ると、重力加速度g は固定の値なので、旋回半径r は飛行速度Vとバンク角θ によって決まるという結果になります。
これが旋回半径の式です。
ここで tanθ はθが大きければ大きいほど、すなわち傾き(バンク)が大きければ大きいほど大きな値になります。
このことから旋回半径r は速度が遅ければ遅いほど、機体の傾きが大きければ大きいほど小さくなると分かります。
逆に速度が速く機体のバンクを小さくして旋回すると、旋回に必要な半径は大きくなるのですが、これは感覚的にも納得できるのではないでしょうか?
実際の飛行記録から旋回の軌跡を測ってみよう!
旋回半径の導き方が分かったところで、今度は実際の飛行記録で旋回半径を見てみたいと思います。
下の画像はとある飛行機が伊丹空港に着陸した際の軌跡です。
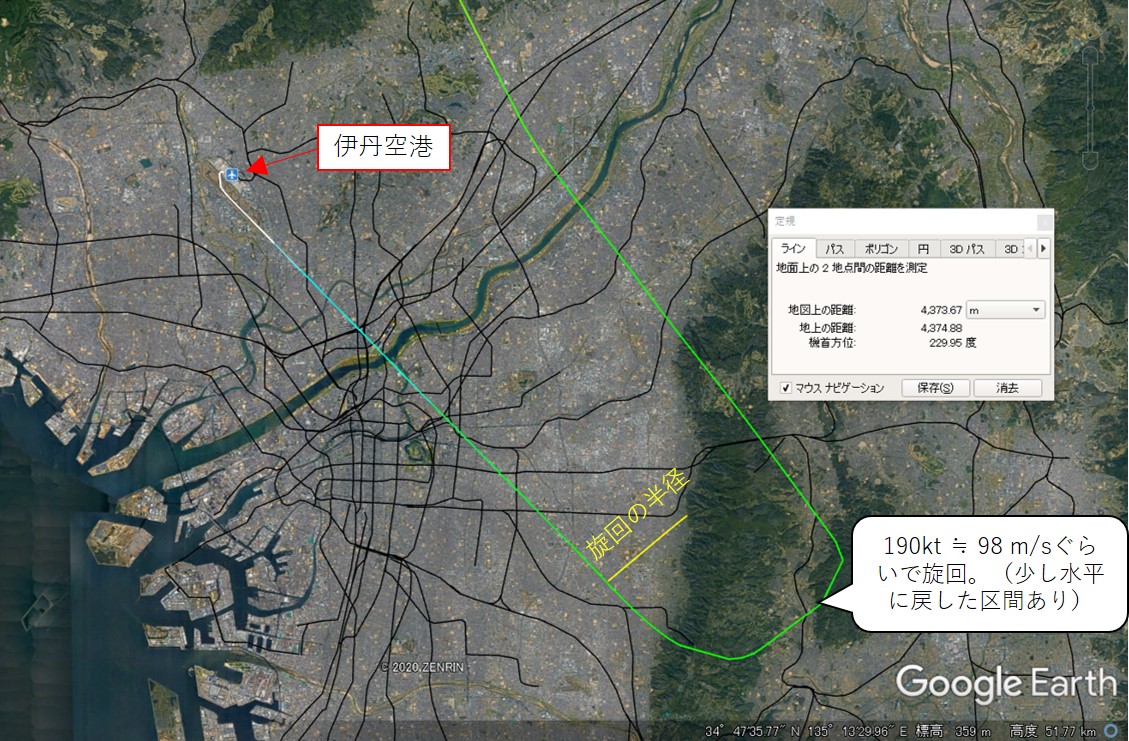
この軌跡では伊丹空港に向けてほぼ180度の旋回を行っていますが、地図上でその半径を測ってみると約4,300mになっています。
ここで先ほど導いた旋回半径の計算結果を比較してみましょう。
記録によれば、この軌跡の旋回では若干速度に変動がありましたが、大体飛行機の速度は地面に対して190kt (98 m/s)ほどでした。
通常、旅客機が旋回をする時は、バンク角は15°からせいぜい20°ほどと言ったところです。
これを踏まえて先ほどの計算式に当てはめてみると、
旋回半径r = (98×98) ÷ (9.8×tan15°) = 3650m
という結果になりました。
軌跡をよーく見ると少しだけ水平飛行に戻した部分があることも考えると、かなり近い値になっていることが分かりますね。
さらにもう1つ例を挙げてみましょう。
今度は福岡空港のすぐ近くで旋回を実施して着陸した際の軌跡です。
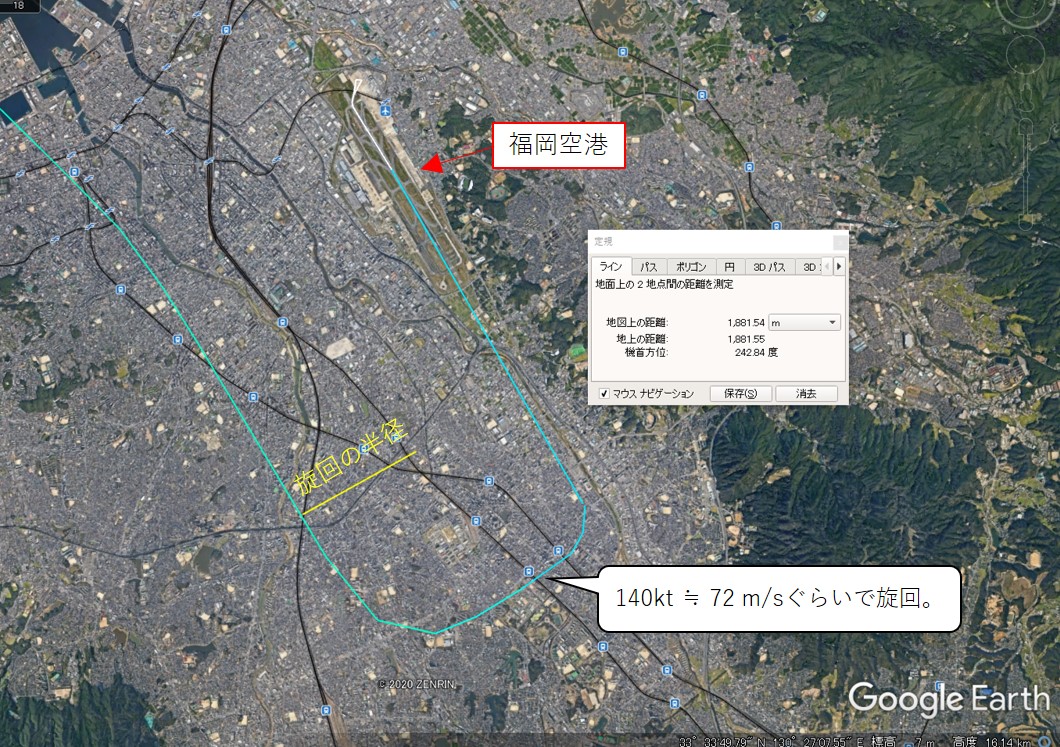
地図上の旋回半径を測ってみると約1,900mとなっています。
この時の旋回速度は大体140kt (72m/s) ぐらいだったので、
旋回半径r = (72×72) ÷ (9.8×tan15°) = 1974m
となります。
着陸間際の旋回ではややバンクが深くなることがありますから、それを考慮するとこれも計算で出した値に近いことが分かりますね。
ところで、飛行機は着陸時の一番遅い時であっても、上の福岡空港の例のように速度は最低でも130~140ktぐらいは出ています。
ということは、飛行機の旋回半径はどんなに小さくても1,500m~2,000mぐらいは必要ということが言えるわけです。
90°向きを変えるだけで1.5~2kmも距離が必要になるのですね。
終わりに
いかがでしたか?
途中の計算式は難しかったかもしれませんが、最終的に飛行機の旋回の大きさは最低でも半径1,500mぐらいになる、ということだけでも興味深いと言えるのではないでしょうか?
実際に数値として出してみると、飛行機の動きのスケールがいかに大きいかが感じられますね。
今後も航空力学を交えた雑学が思い浮かびましたら、がんばって紹介したいと思います。
以上!






