こんにちは。ころすけです。
飛行機の操縦を考える時、失速という現象は常に意識しなければならないものです。
実際、飛行機の操縦マニュアルである飛行規程に定められている様々な速度には、飛行機が失速する速度を基準に決まっているものが多数あります。
しかし失速とは正確にはどういうものなのか、また物理学的にきちんと説明ができるかと問われれば、なかなか難しいと感じる人が多いのではないでしょうか?
というわけで今回は、失速と速度の関係について数学や物理を用いて理論的に考察してみたいと思います。
今回はある程度飛行機の知識がある上級者向けに記事を書いています。
飛行機についてあまり知らないという方は、以下の記事でより簡単に失速と計器指示速度の関係について書いていますので、まずはそちらをご覧ください。

失速は迎角のみの問題で速度は本質的な要素ではない
まず最初に確認しなければならないのは失速という現象とは何か?についてです。
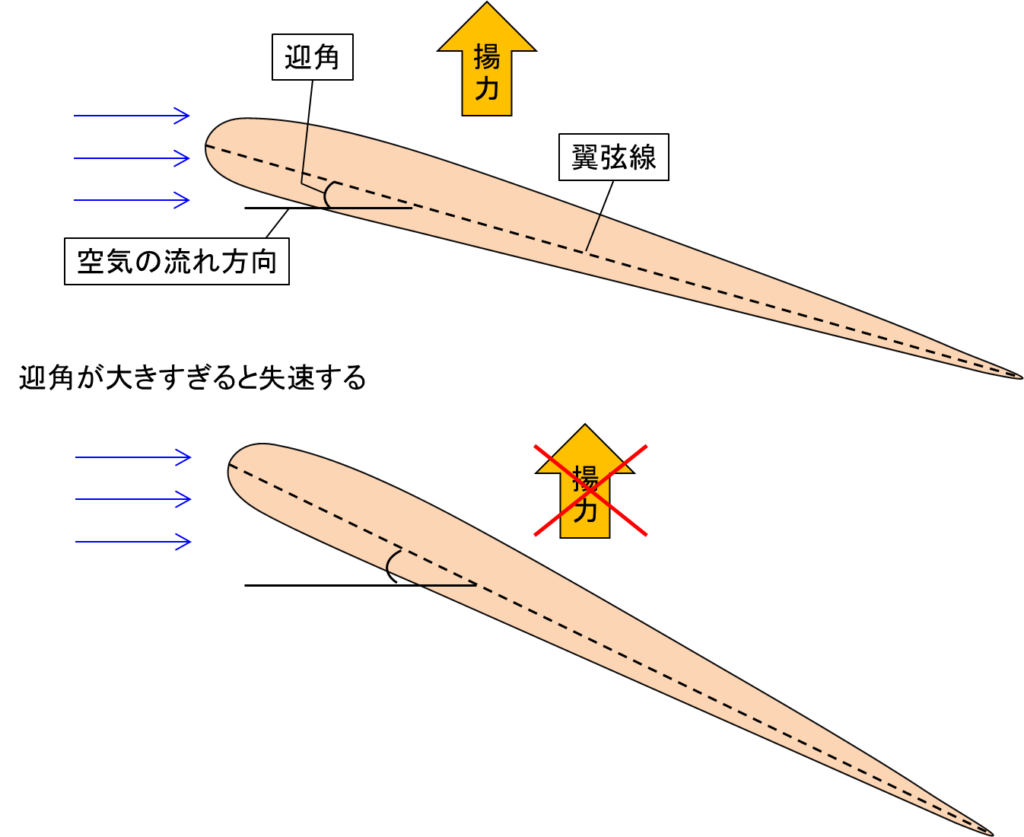
飛行機の翼には飛行中、翼の表面に沿って空気が流れており、この流れによって発生する上下の圧力差によって揚力が生まれています。
この揚力は翼の翼弦線(翼の先端と後端を結んだ線)と気流の成す角度、すなわち迎角を大きくするとより大きくなります。
しかし、揚力を大きくしようと機首を上げて迎角を大きくし過ぎると、ある角度で流れる空気が翼表面に沿ってきれいに流れなくなり、外から見ると気流が翼表面から剥離した状態になってしまいます。
この状態が失速です。
失速状態になると揚力は発生しなくなりますから、飛行中であれば機体の重量を支える力が失われ、機体はストンと落ちるように姿勢を乱してしまいます。
通常であれば適切な回復操作をすれば問題はありませんが、回復が遅れてしまえば最悪の場合墜落に至ります。
また、エアラインなど旅客を乗せて飛行するような場合は不安定な挙動が旅客の安全を脅かすことになるので、失速に入った時点で営業運航としてはNGです。
そんな失速ですが、最も重要なのは以下の点です
それは、「失速は迎角だけの問題であって、速度とは本質的には関係がない」ということです。
これは誤解しがちなので頭においておくと良いでしょう。
ですが実際には失速の兆候に気付く計器上の数値としては速度になります。
これはどういうことでしょうか?
それは通常、計器指示速度と迎角には一対一の関係が成立しているからなのです。
ちょっと見方を変えると、失速の兆候を知るには迎角をモニターしたいところだけど、速度からでも迎角の大きさを判断できるので、速度を使っているとも言えます。
では迎角と速度がどのような理屈で関係付けられているのか、数式を用いて理論的に確認していきましょう。
Step1: 計器指示速度の測定原理を整理しよう
計器指示速度の測定に必要な装置はピトー管と静圧孔
まず始めに、計器に表示される速度がどのようにして計測されているのか確認してみましょう。
計器指示速度は機首部分に取り付けられたピトー管と機体側面に取り付けられた静圧孔から測定されています。
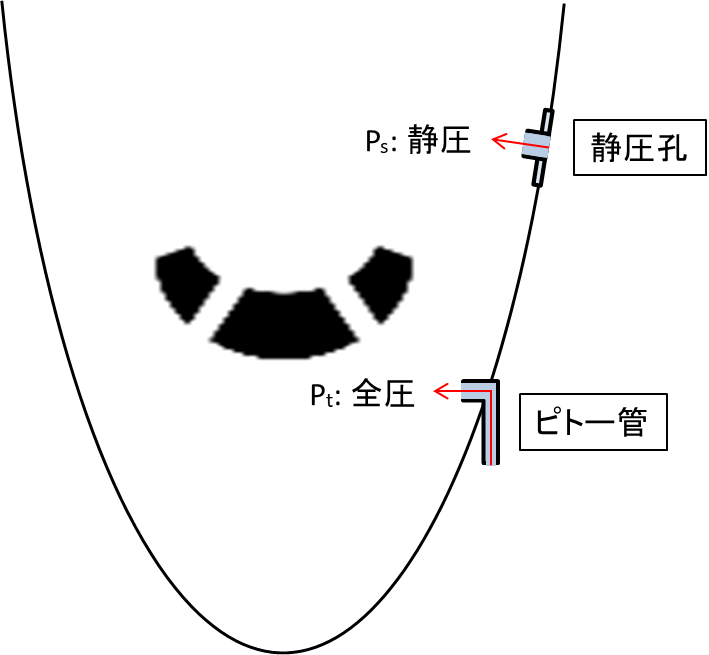
図のようにピトー管は全圧を、静圧孔は静圧という値を測定しているのですが、ここで全圧(Pt)、静圧(Ps)、動圧(Pd)という言葉について確認しましょう。
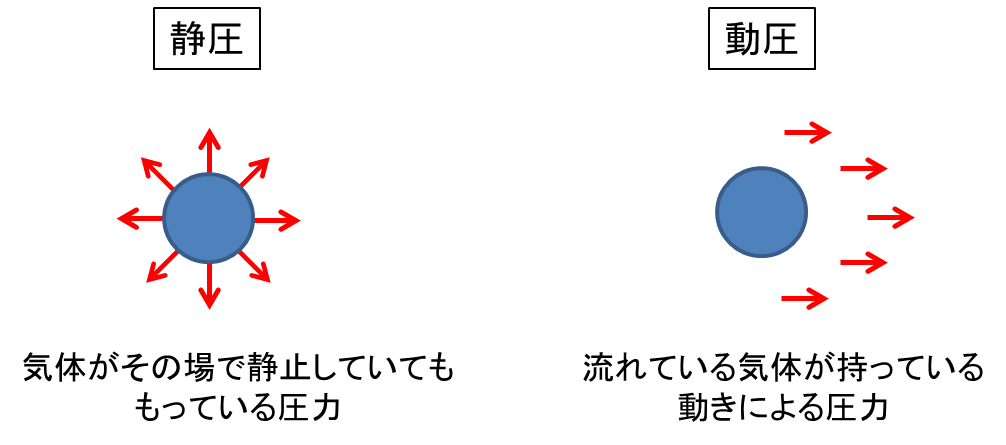
静圧は気体が静止している状態でも持っている圧力を言い、天気図に出てくる気圧も静圧になります。
一方で例えば扇風機の前に立って風を受けると風圧を感じると思いますが、このように流れている気体が持っている動きによる圧力を動圧と言います。
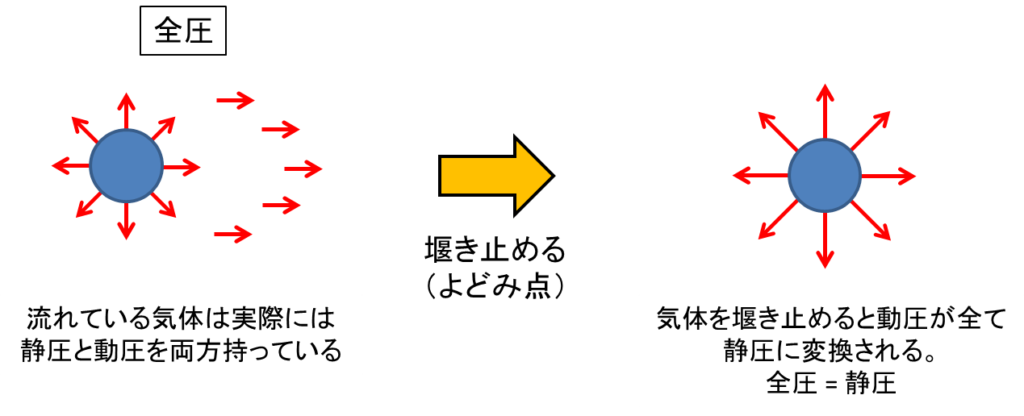
ところで、流れている気体は動圧だけを持っているのかと言うとそうではありません。
流れている気体は動圧と同時に静圧も持っているのです。
このような場合では、動圧と静圧を合計したものが気体が持っている全ての圧力となり、全圧と呼ばれます。
流れている気体は堰き止めてやると動圧がゼロになるのですが、その時に動圧は消えてしまうのではなく、静圧に変換されて全体の圧力としては保存されるのです。
ピトー管は前方から入ってくる空気の流れを最終的に堰き止めて圧力を測定しているので、計測しているのは全圧になるというわけです。
一方で静圧孔は、流れを持った機体が孔に入ってこないように機体側表面に取り付けられていますから、計測されるのは静圧のみになります。
数式を使って計器指示速度を理解しよう
ではここで計測された全圧と静圧を使って、計器に表示する速度がどのように計算されるのかを数式を用いて見ていきます。
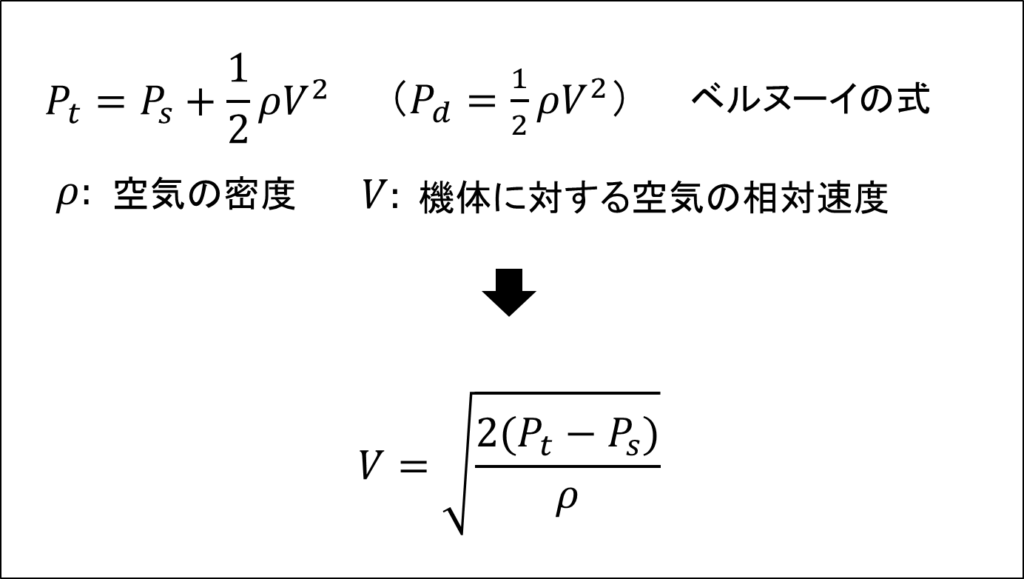
先ほど全圧は静圧と動圧の和であると説明しましたが、それを式で表すと上図のようになり、これはベルヌーイの式と呼ばれています。
さらに動圧は空気の密度と速度の関数として表されるので、式を変形すれば速度は全圧と静圧の差分を求めてやれば算出できることが分かります。
後は空気の密度が分かれば速度が分かるのですが、代入する密度の値によって算出される速度の値は変化します。
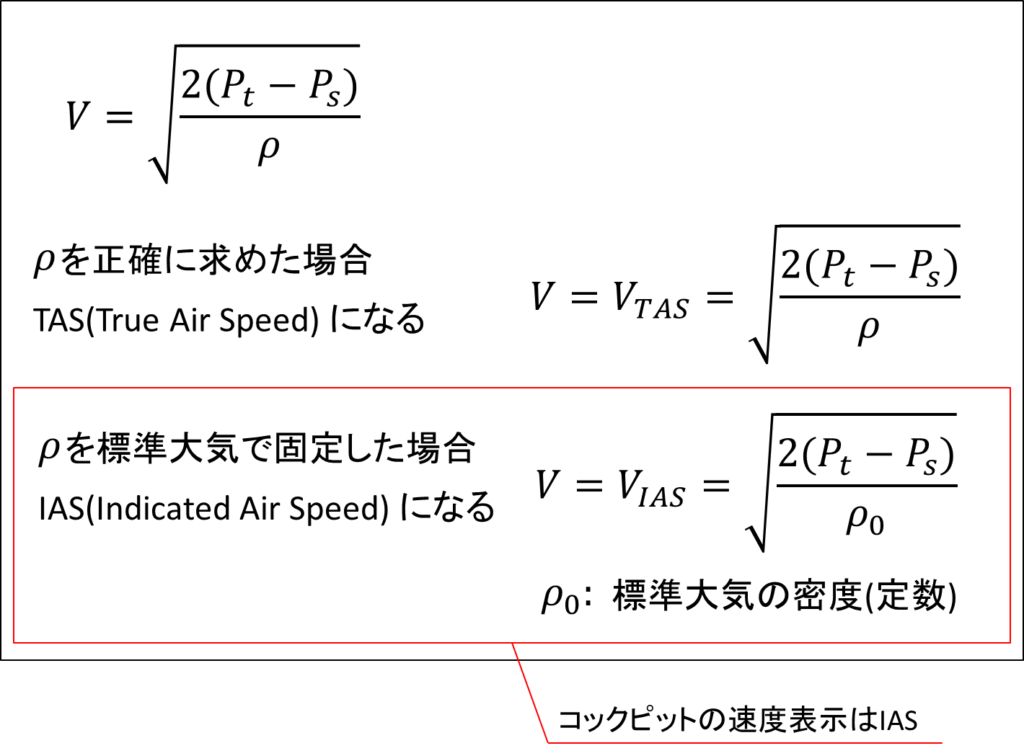
結論から言うと、コックピットの計器で表示されている計器指示速度は機体周辺の正確な密度を用いているわけではありません。
このようにして計測される速度はIndicated Air Speed(IAS)と呼ばれており、計器に表示される速度は実際に機体に対して空気が流れている速度ではないのです。
仮に飛行中の機体周辺の正確な空気密度を用いた場合は、実際に機体に対して空気が流れる速度を表しており、True Air Speed(TAS)と呼ばれます。
この速度は無風状態であれば地上から見た機体の移動速度と一致しますが、もしも空気の密度を正確に測ろうとすると、ピトー管や静圧孔以外に計測装置が必要になります。
計器指示速度ではそこまでせず、密度の値には地上大気の平均的な状態である標準大気の値が使われているというわけです。
Step2: 飛行中の力のつり合いを考えよう
今度は視点を変えて、飛行中に飛行機に働く力のつり合いを考えてみましょう。
下図に示すように飛行機は飛行中、重力による下向きの力に対して釣り合う上向きの力が必要です。
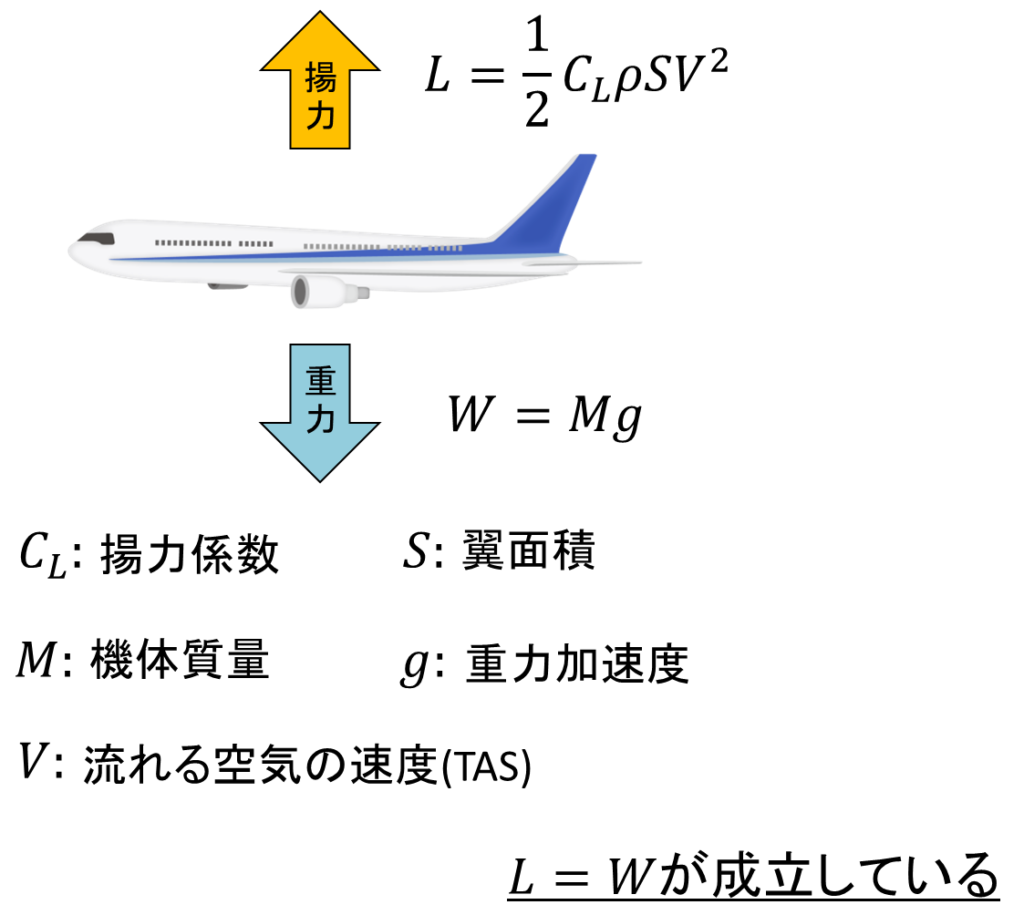
よく飛行機は空に浮くのだから、翼には自重以上の揚力が働いていると誤解されがちですが、飛行機が安定飛行している時の力は必ずつり合い状態にあります。
これは上昇している時も、降下している時も同じです。
なぜならもしも力が釣り合っていないとすると、飛行機はいずれかの方向にどんどん加速していってしまうことになるからです。
飛行機の中で上向きの力となっているのは揚力しかありませんから、揚力Lと重力Wはイコールで結ぶことができます。
ところで、飛行機に発生する揚力は流れる空気の速度(TAS)や揚力係数を用いて上図の式のように表すことができます。
揚力係数は翼の形状や迎角の大きさで決まる値であり、フラップなどを操作して翼の形状を変えない限りは迎角の大きさで決まります。
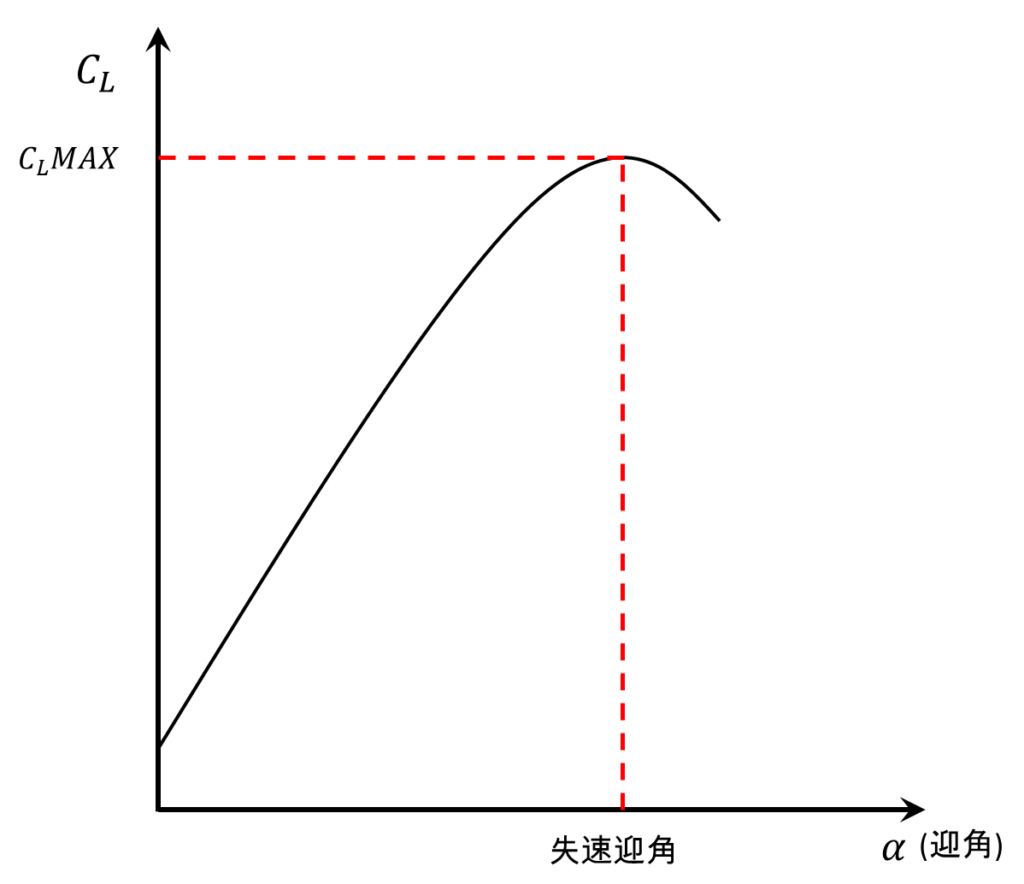
上のグラフのように、揚力係数は迎角を大きくしていくにつれて比例するように大きくなります。
すなわち、機首を上げれば上げるほど大きな揚力を発生させることができるというわけです。
ところが、迎角αを大きくしていくとあるところでそれ以上揚力係数が増大しなくなります。
これはこの角度から翼の表面の気体の流れが剥離し始めていることを意味し、一般的にこの時点で失速と見なすので、失速迎角と言います。
機首を上げられる限界があるということですね。
Step3: 速度の式と力のつり合いの式から速度と迎角の関係を導こう
それではStep1、Step2の数式を使って、失速迎角と計器指示速度の関係を導いてみましょう。
これまでの数式を用いてまとめると以下のようになります。

注目したいのは、TASでなくIASを用いることで、速度を決定する変数が揚力係数だけになっている点です。
揚力係数は迎角によって決まる値ですから、計器指示速度(IAS)は迎角と連動していることが分かります。
すなわち、機体が増速すれば揚力係数は小さくなり(迎角小)、減速すれば揚力係数は大きく(迎角大)なるのです。
飛行機の操作で言えば、増速する時は機首を下げ、減速する時は機首を上げるのです。
このようにIASをコックピットの計器表示とすることで、IASの値によって迎角の大きさを判断することができるのです。
ところで揚力係数にはStep2で見たように最大値があって、それ以上迎角を大きくすると失速してしまいます。
つまり、揚力係数が最大になる速度(IAS)が減速できる限界であり、それ以上減速しようと機首を上げると失速してしまうということなのです。
この速度が失速速度というわけです。
このように、パイロットは計器に表示されたIASに注意を払うことで、失速の兆候を把握することができるのです。
終わりに
いかがでしたか?
航空力学はイメージしづらい部分が多いですが、きちんと順序立てて考えてやれば、かなり理解が深まるのではないかと思います。
最後に補足ですが、上記の理屈は全て機体が安定している場合、もしくは速度や迎角の変化が緩やかな場合を前提としています。
どういうことかと言うと、仮にある速度で飛行している場合に急激に機首上げ操作をした場合を想像してみてください。
この記事でもあるように、機首を上げれば速度は減少していきますが、急激に操作をした場合には速度が減少する前に迎角だけが大きくなります。
この場合、計器上の速度は失速速度以上であっても、実際には失速に陥ってしまう可能性があるのです。
冒頭で述べた通り「失速は迎角だけの問題であって、速度とは本質的には関係がない」のです。
ですが曲技飛行をやる飛行機でもない限り、そのような急激な操作は想定されていないので、通常は速度によって失速の兆候を判断できるというわけです。
以上!






